Jedes Unternehmen, das etwas verkauft, besitzt die Daten für eine Warenkorbanalyse und damit einen wahren Datenschatz. Der Output der Warenkorbanalyse umfasst das gesamte Einkaufsverhalten der Kunden, die Ergebnisse können daher für eine ganze Reihe von Themen hilfreich sein: Preisgestaltung, Regalplatzierung, Sortiment-Auswahl, Katalogdesign, Rabatt-Aktionen, zielgerichtetes Marketing, Up- & Cross-Selling oder die Kundensegmentierung.

In Teil 1 dieser mehrteiligen Blogserie beschäftigen wir uns mit den analytischen Grundlagen zur Warenkorbanalyse und der praktischen Umsetzung in Excel mit relativ kleinen Datenmengen.

Die Warenkorbanalyse besteht aus einer Reihe von Assoziationsverfahren, mit dem Ziel, häufig miteinander gekaufte Produkte oder Produktgruppen zu finden. Die Definition der Warenkorbanalyse ist leider manchmal etwas schwammig, oft wird sie nur mit der Erstellung von Kundenprofilen in Zusammenhang gebracht. Das ist nicht falsch, aber nicht die einzige Einsatzmöglichkeit.

Untersucht wird im Grunde, wie oft jedes Produkt mit jedem anderen in einem Warenkorb gelandet ist. Es sollen jene Produkte gefunden werden, die den Kauf anderer Produkte implizieren. Dazu werden sogenannte Assoziationsregeln aufgestellt, wie z.B.:

Wenn ein Gast den Ceasar Salad bestellt, dann bestellt er zu 36% ein Mineralwasser.

Übrigens ein gutes Beispiel dafür, dass die Warenkorbanalyse nicht nur im Einzelhandel von Bedeutung ist, sondern im Grunde in jedem Geschäftsumfeld Sinn macht. Die Analyse geht dann noch weiter:

• Es werden sinnvolle Produktgruppen gebildet, also Artikel die häufig miteinander gekauft worden sind
• Es werden alle Regeln gefunden, auch die exotischsten, auf die kein Mensch kommen würde
• Für jede Regel werden Kennzahlen berechnet, damit die Spreu vom Weizen getrennt werden kann

Verglichen mit dem Nutzen einer Warenkorbanalyse ist der Aufwand relativ klein. Und seit einigen Jahren ist die Analyse in Standardsoftware sogar noch einfacher durchzuführen.

Analytische Grundlagen

Die Datenbasis für die gesamte Analyse bilden die Transaktionen, also die Warenkörbe. Ein klassisches, aber einfaches Beispiel zur Illustration soll eine Trafik sein, in der folgende Rechnungen vorliegen:

• Re.1: Zigaretten, Feuerzeug, Glückslos
• Re.2: Zigaretten
• Re.3: Zigaretten, Tageszeitung, Wochenmagazin, Glückslos, Parkschein
• Re.4: Zigaretten, Wochenmagazin
• ...

Die Rohdaten müssen aufbereitet werden, damit sie in geeigneter Form zur Analyse vorliegen. In Excel können die Daten beispielsweise mit einer Pivot-Tabelle so aufbereitet werden, dass jede Transaktion eine Zeile dars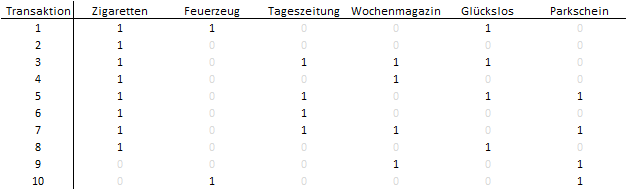tellt:

Jede Zeile ist ein Warenkorb, z.B. die erste Zeile repräsentiert Rechnung 1: Zigaretten, Feuerzeug, Glückslos. Ob ein Produkt gekauft wurde, ist mit 0/1 kodiert (0 = nicht gekauft, 1 = gekauft), damit einfach Summen gebildet werden können. Mit diesen Daten können die drei zentralen Kennzahlen der Warenkorbanalyse berechnet werden: Support, Konfidenz und Lift. Wir knöpfen uns mal die beiden Produkte vor, die erwartungsgemäß am stärksten zusammenhängen, nämlich Zigaretten und Feuerzeug.

Support

Der Support soll die einfache Frage beantworten, wie oft ein Produkt überhaupt gekauft wurde. Betrachten wir dazu die ersten beiden Spalten getrennt voneinander: es wurden 8 mal Zigaretten gekauft und 2 mal Feuerzeuge. Bei 10 Transaktionen ist das ein Support von respektive 80% und 20%. Wir oft wurden aber beide zusammen gekauft? Nur einmal (Transaktion 1), also nur ein Support von 10%. Fassen wir also den Support zusammen:

• Support(Zigaretten) = 80%
• Support(Feuerzeug) = 20%
• Support(beide) = 10%

Konfidenz

Die Konfidenz sagt aus, wie oft ein Feuerzeug gekauft wird, wenn Zigaretten gekauft werden. Es wurden 8 mal Zigaretten gekauft, davon einmal mit Feuerzeug, die Konfidenz liegt also bei 1/8 = 12,5%. Die Konfidenz lässt sich auch aus dem Support berechnen:

• Konfidenz = Support(beide) / Support(Zigaretten)
• Konfidenz = 10% / 80% = 12,5%

Die Konfidenz wird zur Formulierung der Regel herangezogen, denn sie sagt aus, wie "sicher" die Regel ist:

Wenn Zigaretten gekauft werden, wird zu 12,5% auch ein Feuerzeug gekauft.

Das ist natürlich kein besonders guter Wert, denn es wird nicht sonderlich häufig ein Feuerzeug zusammen mit Zigaretten gekauft. Um die Analyse abzurunden gibt es noch eine weitere Kennzahl, den Lift.

Lift

Die Frage hier ist: um wie viel wahrscheinlicher machen Zigaretten den Kauf eines Feuerzeugs? Hier die Formel und die Berechnung dazu:

• Lift = Support(beide) / (Support(Zigaretten) * Support(Feuerzeug))
• Lift = 10% / (80% *  20%) = 62,5%

Vorsicht bei der Interpretation: ein Lift von 62,5% heißt nicht, dass Zigaretten den Kauf eines Feuerzeugs um 62,5% wahrscheinlicher machen. Sie müssen den Lift als multiplikativen Faktor verstehen: ein Lift von 200% bedeutet, dass sich die Wahrscheinlichkeit für das Feuerzeug verdoppelt, ein Lift von 300% dass sie sich verdreifacht usw. Der Referenzwert ist 100%, alles darüber ist gut und alles darunter ist schlecht. Ein Lift von beispielsweise 150% bedeutet , dass die Wahrscheinlichkeit für ein Feuerzeug um 50% steigt. Unser Lift liegt aber 37,5% unter den 100%, das heißt daher:

Wenn Zigaretten gekauft werden, wird die Wahrscheinlichkeit ein Feuerzeug zu kaufen um 37,5% kleiner.

Das passt ja auch zur schlechten Konfidenz oben, ist aber eine wesentlich härtere Aussage. Das Beispiel ist bewusst so gewählt, um die Ergebnisse besser zu verstehen. Der Grund für die schlechten Kennzahlen liegt in den Daten. Es gibt nämlich auch einen Warenkorb (der letzte oben), in dem ein Feuerzeug ohne Zigaretten gekauft wurde. Auch wenn es nur ein einziger Fall ist, er macht die Hälfte der Feuerzeug-Käufe aus (das waren ja nur zwei). Hier offenbart sich das Problem zu geringer Datenmengen. Für eine sinnvolle Analyse sollten mindestens einige hundert, besser einige tausend Transaktionen vorliegen.

Nichtsdestotrotz, die Kennzahlen (Support, Konfidenz und Lift) stimmen, denn sie drücken kurz und prägnant aus, wie viel die Regel eigentlich wert ist. Dazu nun ein etwas erfreulicheres Beispiel aus dem selben Datensatz, nämlich zu Zigaretten und Glückslosen. Spielt man die Berechnungen nochmal durch findet man folgende Ergebnisse:

• Support(Zigaretten) = 80%
• Support(Glückslos) = 40%
• Support(beide) = 40%
• Konfidenz = 40% / 80% = 50%
• Lift = 40% / (80% * 40%) = 125%

Wenn Zigaretten gekauft werden, wird zu 50% auch ein Glückslos gekauft (Konfidenz). Die Wahrscheinlichkeit für das Glückslos steigt durch die Zigaretten um 25% (Lift).

Der Trafikant sollte Zigaretten-Käufern also kein Feuerzeug anbieten, sondern ein Glückslos!

In die Analyse fließen nicht nur die Häufigkeiten ein, mit denen zwei Produkte zusammen gekauft worden sind, sondern auch wie oft sie nicht zusammen gekauft worden sind. Nur damit kann wirklich objektiv bemessen werden, was wertvolle Regeln des Kaufverhaltens sind.

Verfahren zur praktischen Bewältigung

Die eigentliche Problematik der Warenkorbanalyse ist der Rechenaufwand bei vielen Produkten. Support, Konfidenz und Lift sind zwar einfach zu berechnen, aber man muss das ganze ja für jedes mögliche Produktpaar wiederholen. Im Beispiel vorher wurde nur untersucht, welchen Effekt Zigaretten auf Feuerzeuge haben und auf Glücklose. Nun wäre noch interessant zu wissen welchen Effekt Zigaretten auf die anderen Produkte haben und dann nochmal das ganz umgekehrt: welchen Effekt haben denn Glücklose auf Zigaretten und welchen haben Feuerzeuge auf Zigaretten?

Man kann aus der Anzahl der angebotenen Produkte berechnen, wie viele Kombinationen sich ergeben: bei 10 Produkten gibt es 55 Kombinationen, bei 100 Produkten gibt rund 5.000 Kombinationen, bei 1.000 Produkten gibt es über 500.000 Kombinationen! Es ist unmöglich, das "händisch" durchzurechnen, daher gibt es automatisierte Verfahren dafür. Im Wesentlichen sind das drei unterschiedliche Zugänge, allesamt auf Basis derselben Daten, also der Warenkörbe.

Die einfachste und schnellste Variante ist die Korrelationsanalyse in Excel, die eine erste Annäherung bringen kann, jedoch nicht ganz vollständig ist. Eine vollständige Untersuchung aller Regeln ist im Apriori-Algorithmus abgebildet, der allerdings nicht in Excel verfügbar ist. Und darüber hinaus gibt es noch die Clusteranalyse, die Produkte zu Gruppen zusammenfasst und damit eine zusätzlichen Blickwinkel auf das Kaufverhalten der Kunden ermöglicht.

Korrelationsanalyse in Excel

Zunächst aber zu den Grundlagen der einfachsten Variante, die Korrelationsanalyse. Der Korrelationskoeffizient ist   eine Zahl zwischen 0 und 1, die ausdrückt wie stark zwei Produkte zusammenhängen:

• Korrelation = 0 bedeutet kein Zusammenhang
• Korrelation = 1 bedeutet perfekten Zusammenhang
• Korrelation mit positivem Vorzeichen steht für positiven Zusammenhang (je mehr, desto mehr)
• Korrelation mit negativem Vorzeichen steht für negativen Zusammenhang (je mehr, desto weniger)

In Excel wird die Formel KORREL() dafür verwendet, wie hier am Beispiel von Zigaretten und Glücklose gezeigt:

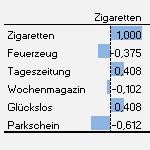
Der Wert der Korrelation liegt bei 0,408. Das bedeutet, dass es eine positiver Zusammenhang ist und dass er im mittleren Bereich liegt zwischen 0 und 1, also in Worte gefasst:

Es gibt einen mittleren Zusammenhang zwischen Zigaretten und Glückslosen: je mehr Zigaretten, desto mehr werden auch tendenziell Glückslose gekauft.

Der Korrelationskoeffizient von Zigaretten und Feuerzeug liegt dagegen bei -0,375. Das ist ein etwas schwächerer Zusammenhang, und er ist negativ. Das heißt also:

Es gibt einen leicht negativen Zusammenhang zwischen Zigaretten und Feuerzeugen: je mehr Zigaretten, desto weniger werden Feuerzeuge gekauft.

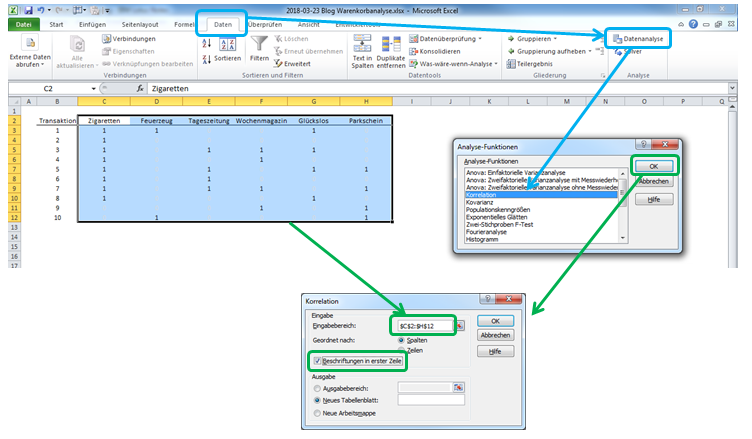
Die Ergebnisse der Korrelationsanalyse sind also im Einklang mit den Ergebnissen zu Support, Konfidenz und Lift. Es ist im Grunde nur eine alternative Betrachtungsweise, allerdings ohne harte Zahlen zu Wahrscheinlichkeiten (der Korrelationskoeffizient kann nicht als Wahrscheinlichkeit interpretiert werden). Der wesentliche Vorteil der Korrelationsanalyse ist die Einfachheit der Berechnung. In Excel können mit wenigen Klicks alle Produktpaare mit erfasst werden können. Im Registerblatt Daten klicken Sie auf Datenanalyse, dann im pop-up Korrelationen auswählen und auf OK. Im zweiten pop-up ist der Eingabebereich anzugeben (inklusive Überschriften) und das Hakerl zu setzen bei Beschriftungen in erster Zeile.

Es entsteht ein neues Sheet mit der sogenannten Korrelationsmatrix. Das ist eine Tabelle, die für jedes Produkt die Korrelationen zu allen anderen Produkt beinhaltet:

Lese-Bsp. zu Spalte 1 (Zigaretten): Die Korrelation von Zigaretten mit Feuerzeugen liegt bei -0,375, von Zigaretten mit Tageszeitungen bei 0,408, von Zigaretten mit Wochenmagazinen bei -0,102, usw.

Eine Bemerkung: der erste Eintrag ist die Korrelation von Zigaretten mit Zigaretten, also 1,000. Das wiederholt sich für jedes Produkt und ist immer 1,000. Rechts über diesen Einsern gibt es keine Ausgabe, weil sich die Werte auch nur wiederholen würden: die Korrelation von Zigaretten mit Feuerzeugen ist -0,375 und die von Feuerzeugen mit Zigaretten natürlich dasselbe.

Interessant sind nun die hohen Korrelationen, wie z.B. die Von Zigaretten mit Tageszeitungen und die schon vorhin gefundenen von Zigaretten und Glücklosen. Für die hohen positiven Korrelationen gilt: wenn Zigaretten gekauft werden, dann auch Tageszeitungen und Glückslose. Dann gibt es noch die hohen negativen Korrelationen, wie z.B. von Zigaretten und Parkscheinen. Das bedeutet, wenn Zigaretten gekauft werden, werden Parkscheine nicht gekauft.

Fazit

Die Korrelationsanalyse bietet also mit wenigen Klicks eine erste Übersicht zu allen Produkten. Sie ist ein einfaches Tool, um schnell zu identifizieren wo die höchsten Zusammenhänge liegen. In Teil 2 und 3 dieser Blogserie zur Warenkorbanalyse wird gezeigt, wie man wesentlich größere Datenmengen handhaben kann. Dazu wird die Korrelationsanalyse nochmal aufgegriffen und dann weitere, hoch effiziente Verfahren vorgestellt, um das Kaufverhalten Ihrer Kunden bis ins kleinste Detail zu beleuchten.

Links

Warenkorbanalyse Teil 1: Analytische Grundlagen und Korrelationsanalyse in Excel
Warenkorbanalyse Teil 2: Apriori Algorithmus in R und Power BI
Warenkorbanalyse Teil 3: Clusteranalyse und Kundensegmentierung